「回帰」という言葉がよくわからない、また「線形回帰」って何やねん?と疑問に思ったことはありませんか?実は、線形回帰は教師あり学習の中でも非常に基本的で理解しやすい手法の一つです。本記事では、線形回帰の基本的な概念と使い方について、初心者にもわかりやすく解説していきます。データ分析や機械学習に興味がある方、線形回帰を学びたいけどイマイチピンとこない方にお勧めです。さあ、線形回帰の世界を一緒に探検してみましょう!
線形関係
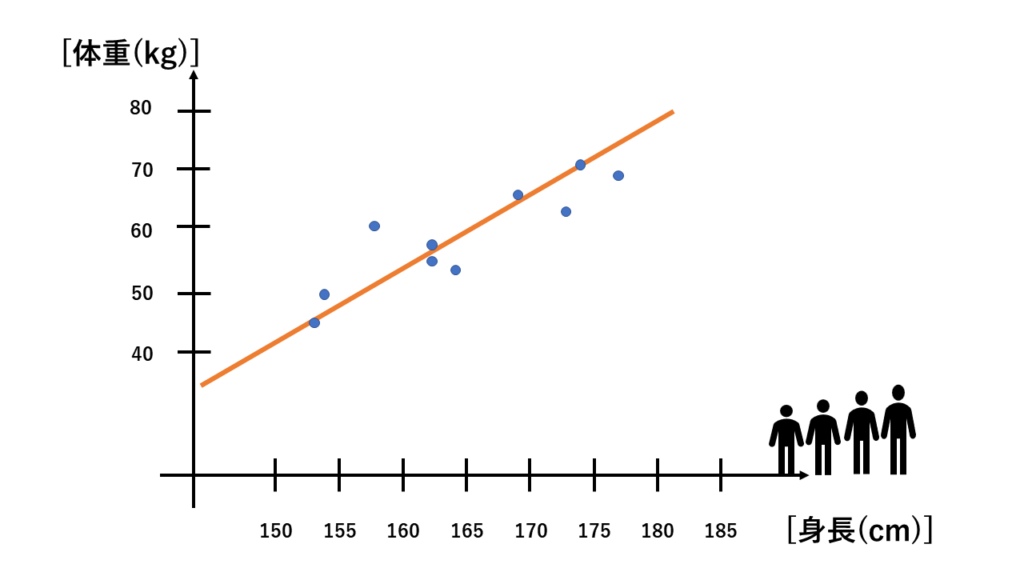
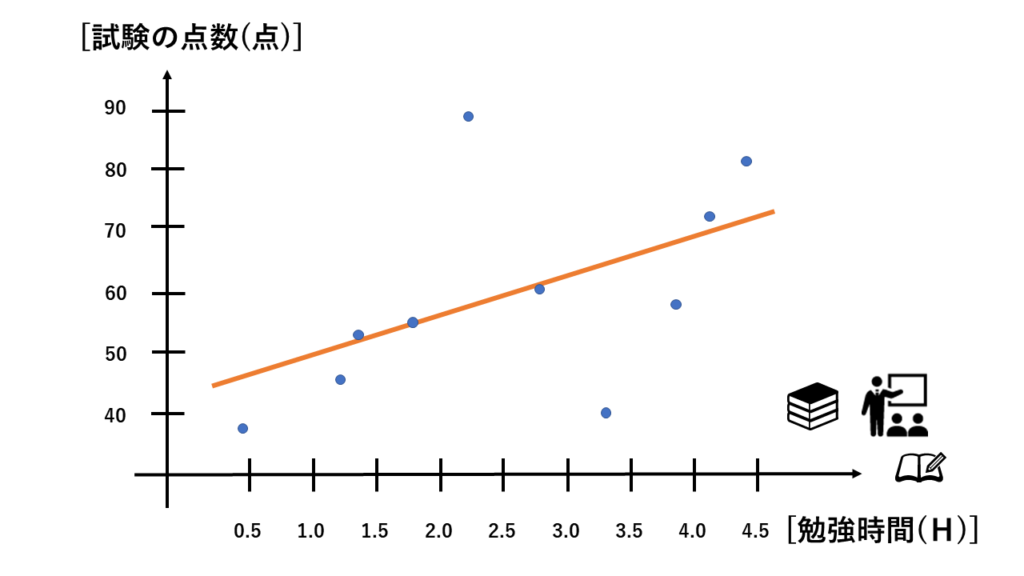
線形回帰は、二つの変数の間に直線的な関係がある場合に使用される統計的な手法です。例えば、身長と体重の関係や、学習時間と試験の点数の関係などが線形関係にあたります。線形関係は、一方の変数が他方の変数に比例的に変化する関係を示しており、その傾きと切片を使って直線的な予測モデルを作成することができます。線形回帰は、このような線形関係を利用して、説明変数と目的変数の間の関係をモデル化し、未知のデータに対して予測を行うことができます。線形回帰は単純なモデルでありながら、実用的な予測モデルとして広く用いられています。
モデルの目的
線形回帰モデルの目的は、与えられたデータに基づいて、説明変数(入力変数)と目的変数(出力変数)の間の線形関係をモデル化し、予測を行うことです。つまり、与えられたデータを元に、説明変数の値を入力することで、目的変数の予測値を得ることができます。前の例で表しますと、身長から体重を予測する、勉強時間から試験の点数を予測する感じです。線形回帰モデルは、説明変数と目的変数の間の関係を数学的な式で表現し、その式のパラメータ(傾きや切片)をデータから学習することで、未知のデータに対して予測を行います。モデルの目的は、与えられたデータに対して適切な予測を行い、データの背後にある関係性を理解することにあります。
モデルの概要
線形回帰モデルは、与えられたデータに基づいて、説明変数と目的変数の間の線形関係をモデル化します。モデルは一般的に以下のような構成要素で概要されます。
- 説明変数(入力変数):データ中の特徴量や属性を表します。例えば、商品の価格や広告費などが説明変数となります。
- 目的変数(出力変数):予測したい値や目的の値を表します。例えば、売上や需要などが目的変数となります。
- パラメータ:モデルの予測式における傾きや切片の値を表します。これらのパラメータは学習によって最適化され、モデルの予測性能を向上させます。
- 予測式:説明変数とパラメータを組み合わせた式で、目的変数の予測値を計算します。一般的には、説明変数とパラメータの線形結合によって予測値を得ます。
モデルの概要は、データを入力として受け取り、予測式を用いて目的変数の予測値を出力するという流れになっています。学習によって最適なパラメータを見つけ出し、未知のデータに対して予測を行うことが特徴です
パラメータの説明
線形回帰モデルにおけるパラメータは、予測式における傾きと切片を表します。一般的に、線形回帰モデルは以下のような予測式を用います:
y = β0 + β1 * x1 + β2 * x2 + … + βn * xn
ここで、yは目的変数の予測値、x1, x2, …, xnは説明変数の値、β0, β1, β2, …, βnはそれぞれの説明変数に対するパラメータであり、傾きを表します。β0は切片を表し、x1, x2, …, xnの値が0の場合に、予測値yが取る値を決定します。β1, β2, …, βnは各説明変数の影響の大きさを示し、値が大きいほど、対応する説明変数の影響が大きいことを意味します。
パラメータはモデルの学習によって最適化されます。学習データを用いて、予測式のパラメータを調整し、目的変数との誤差を最小化するようにパラメータを更新していきます。最適なパラメータが見つかると、モデルは学習が終了し、予測のために新しいデータに対してパラメータを用いて予測を行います。
パラメータはモデルの重要な要素であり、データに合わせて最適化されることで、モデルの予測性能を高める役割を果たします。また、パラメータの値によって、予測式の形状や予測結果が変化するため、適切なパラメータの選択や調整がモデルの性能を左右する重要な要素となります。
学習と予測
線形回帰モデルの学習は、訓練データを用いてモデルのパラメータを最適化するプロセスです。まず、訓練データを用いて予測式のパラメータを初期化します。次に、訓練データを入力として与え、実際の目的変数の値とモデルの予測値の誤差を計算します。誤差を最小化するようにパラメータを更新し、このプロセスを繰り返してモデルの予測性能を向上させます。
一般的に、最小二乗法が使用されます。これは、目的変数とモデルの予測値の誤差を二乗して足し合わせ、その総和を最小化するようにパラメータを調整する方法です。最小二乗法により、訓練データに最もフィットするようなパラメータが見つかります。
学習が終了した後には、訓練データに対する予測性能を評価するために、モデルの評価が行われます。また、新しいデータに対しての予測を行うこともできます。予測は、学習で得られた最適なパラメータを用いて、新しい説明変数の値を入力として与え、予測式によって目的変数の値を予測するプロセスです。
学習と予測は、線形回帰モデルの主要な機能であり、モデルの予測性能を高めるために重要な役割を果たします。適切な学習データの選択や、モデルのハイパーパラメータの調整などが予測性能に影響を与えるため、丁寧なモデルの学習と予測のプロセスが必要となります。
モデルの評価
線形回帰モデルの評価は、学習が終了した後に、モデルの予測性能を評価するために行われます。評価は、訓練データに対するモデルの予測性能を測定し、モデルが実際のデータに対してどれだけ良い予測を行えるかを評価します。
一般的に、モデルの評価にはいくつかの指標が使用されます。例えば、平均二乗誤差(MSE)や平均絶対誤差(MAE)などがあります。これらの指標は、モデルの予測値と実際の目的変数の値との誤差を計算し、誤差が小さいほどモデルの予測性能が高いと言えます。
また、クロスバリデーションと呼ばれる手法を用いて、モデルの汎化性能を評価することもあります。クロスバリデーションでは、データを複数のフォールドに分割し、一部のフォールドを検証データとして使用し、残りのフォールドを訓練データとして使用します。これを繰り返し行い、モデルの性能を評価します。
モデルの評価は、モデルの性能を客観的に評価し、モデルの改善やハイパーパラメータの調整などのための情報を提供します。適切な評価指標の選択や、クロスバリデーションの適用などが重要であり、モデルの予測性能を正確に評価するために注意が必要です。
線形回帰モデルの応用例
線形回帰は、多くの応用例で使用されます。例えば、以下のような場合に利用されることがあります。
- 住宅価格の予測: 線形回帰は、住宅価格といった目的変数と、部屋の数や面積などの説明変数との間の線形関係をモデル化することができます。これにより、不動産業界などでの住宅価格の予測や、不動産投資の意思決定などに活用されます。
- 売上予測: 線形回帰は、過去の売上データや広告費などの説明変数を用いて、将来の売上を予測するために使用されることがあります。これにより、企業の売上予測や販売戦略の最適化などが可能となります。
- 金融分析: 線形回帰は、金融分析においても広く利用されています。例えば、株価や為替レートの予測、信用スコアの予測、リスク分析などに線形回帰が使用されることがあります。
- 医療分野: 線形回帰は、医療分野においても応用されます。例えば、患者の年齢や血圧などの説明変数を用いて、病気の進行度や治療効果の予測を行うことがあります。
- 社会科学研究: 線形回帰は、社会科学研究においても使用されます。例えば、教育や経済の分野において、所得や学歴などの説明変数を用いて、効果の評価や政策の予測を行うことがあります。
これらは線形回帰の一部の応用例であり、実際には多岐にわたります。線形回帰は、データの傾向を把握し、予測や分析を行うための強力なツールとして広く利用されています。
まとめ
以上で線形回帰モデルについての解説を終わります。線形回帰について理解できたでしょうか?
線形回帰は幅広い応用例があり、今後もデータ分析や予測分析、機械学習の分野での活用が期待されるでしょう。特に、データ量の増加や複雑なデータの解析において、線形回帰は重要な手法として注目されています。今後は、より高度な線形回帰の応用や改良、非線形回帰手法との組み合わせなどが進展することが期待されています。




コメント