勾配降下法(Gradient Descent)とは、数学的最適化の手法の一つであり、関数の最小値(または最大値)を見つけるために使用される手法です。特に、機械学習やディープラーニングにおいては、モデルのパラメータを最適化するために頻繁に利用されます。
この記事では、勾配降下法の種類やパラメータ更新の手順などを解説していきます。しっかり理解してデータ解析や機械学習モデルのトレーニングに活用していきましょう!

勾配降下法の基本概念

勾配降下法は、機械学習や最適化の分野で広く使用される最適化アルゴリズムの一つです。主な目的は、最小化または最大化したい関数(損失関数やコスト関数など)の最適なパラメータを見つけることなどです。
ここでは損失関数が最小となる値を求めることを目的としましょう。
損失関数とは予測した値と実際の正解の値との差を求める関数です。つまり、損失関数の値が小さくなるほど正しい値に近づいていくことができます。
基本的に損失関数は、二乗誤差などで2次関数で表されます。損失関数の値をLとして調整したいパラメータの値をwとすると以下のようなグラフで表すことができます。
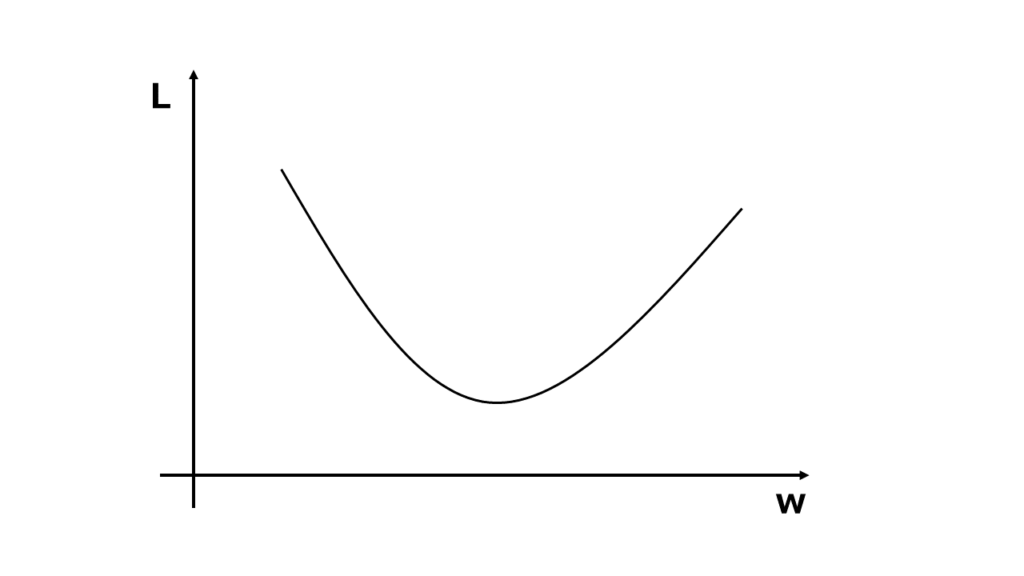
勾配降下法とはこの2次関数で表された坂(勾配)を下って(降下して)いき最適なパラメータを求める方法です。
上図のような谷が1つしかないグラフは最適解を求めるのが簡単なんですが、谷が2つ以上あるようなグラフもあり、最適解ではない谷(局所解)を求めてしまうことがあります。
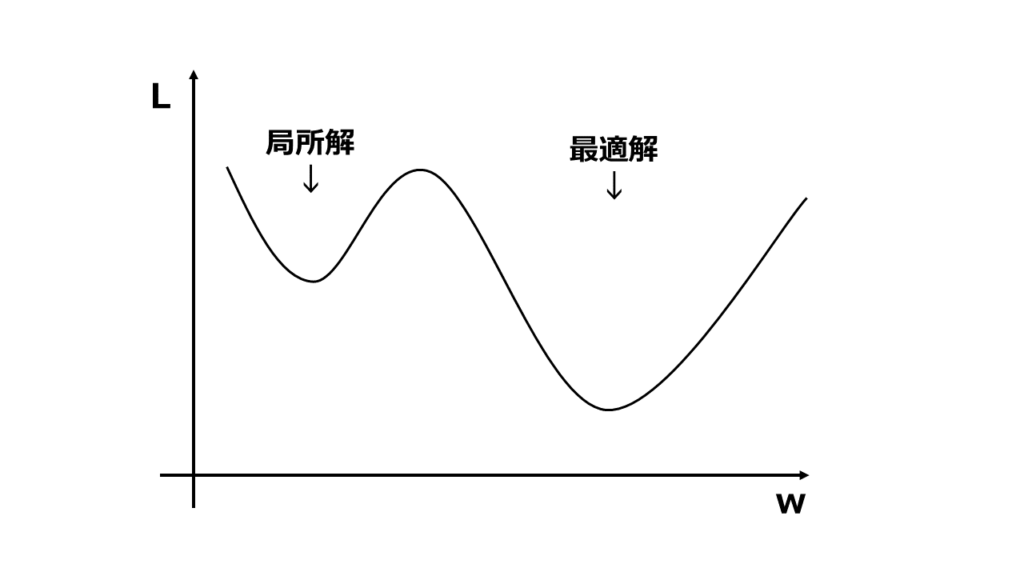
この局所解に惑わされないように最適解を求める方法がいくつかあるので学んでいきましょう!
勾配降下法の手順

ではまずは基本的な勾配降下法で最適解を求める方法を紹介します。
手順1 パラメータの初期値を設定する
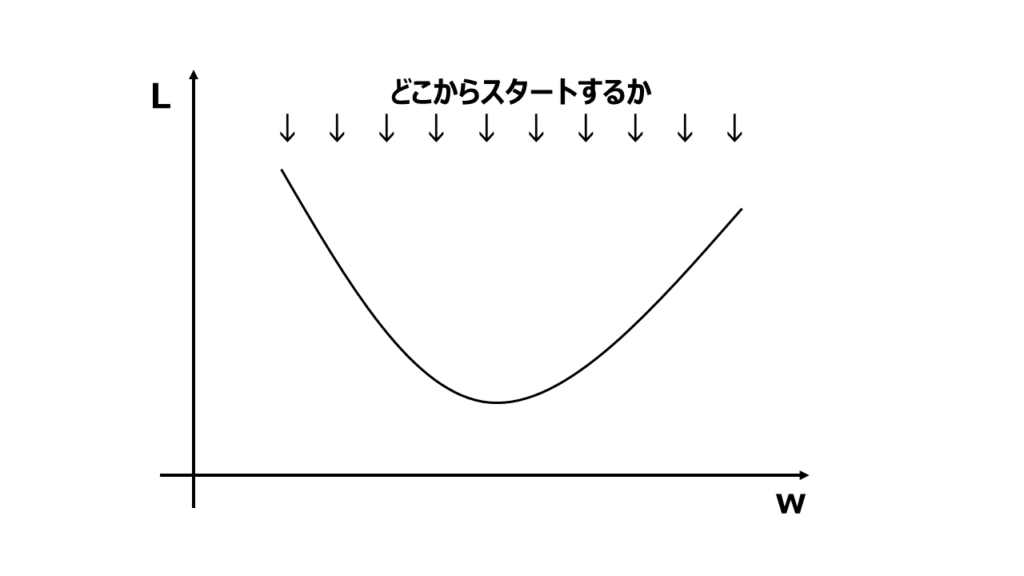
まずパラメータの初期値を設定します。これは通常ランダムな値や0で初期化されます。
どこから山を下り始めるかを最初に決めておきましょう。
手順2 損失関数の勾配を計算
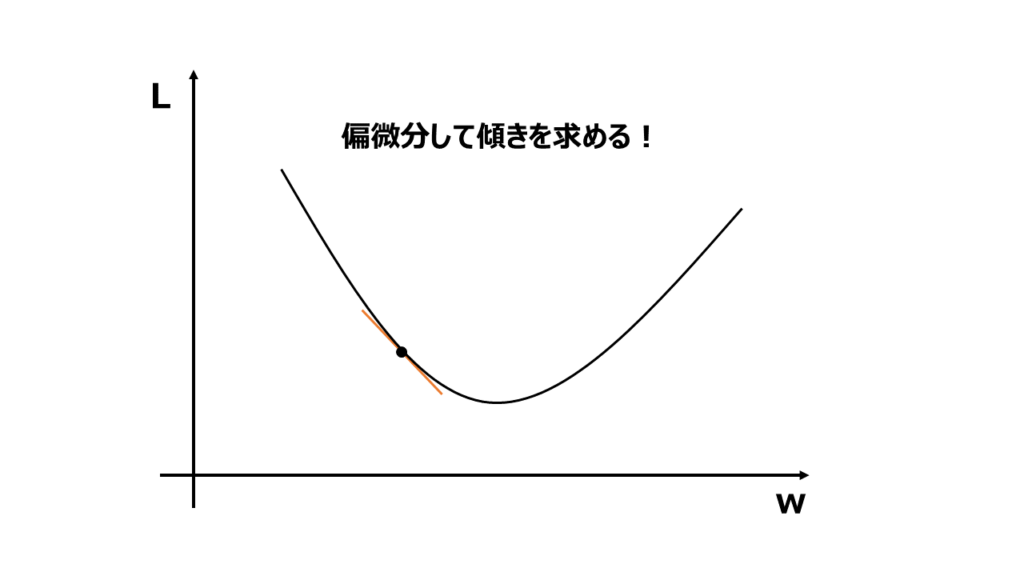
次に現在のパラメータにおける損失関数の勾配(傾き)を計算します。勾配は各パラメータに対して偏微分で求めることができます。
手順3 パラメータの更新
求めた勾配を使用して、パラメータを更新します。一般的な更新式は、以下で表すことができます。
新しいパラメータ = 現在のパラメータ – 学習率 × 勾配
学習率は、パラメータをどれだけ大きく更新するかを制御するハイパーパラメータです。詳しく知りたい方は学習率について解説した記事がありますので是非ご覧ください

手順4 収束させる
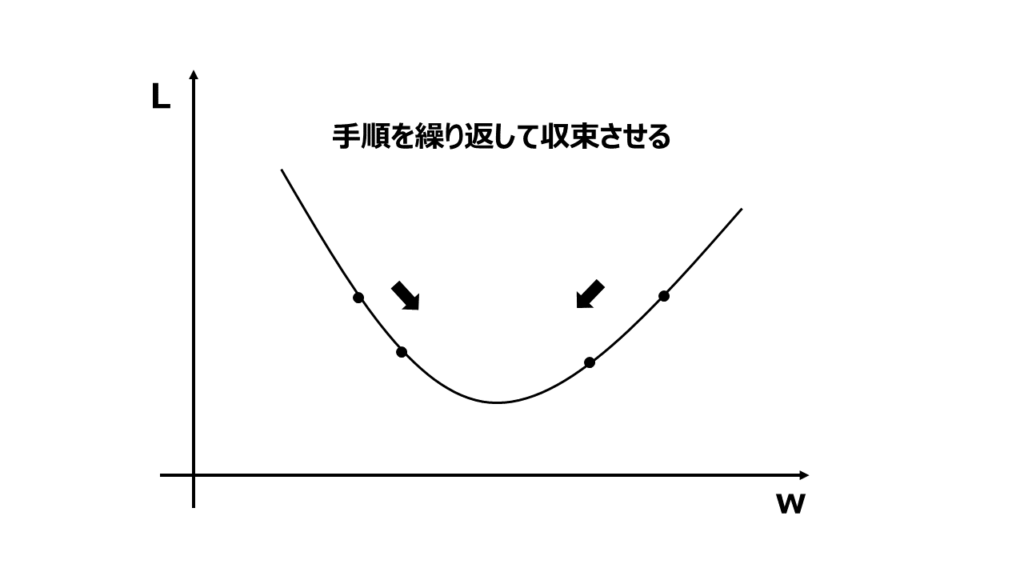
パラメータの値が収束したかチェックします。収束していない場合は手順2から4を繰り返します。
収束チェックには収束条件を設定します。収束条件は、例えば指定したエポック数や損失関数の変化量ンの閾値などです。
手順5 最終的なパラメータの出力
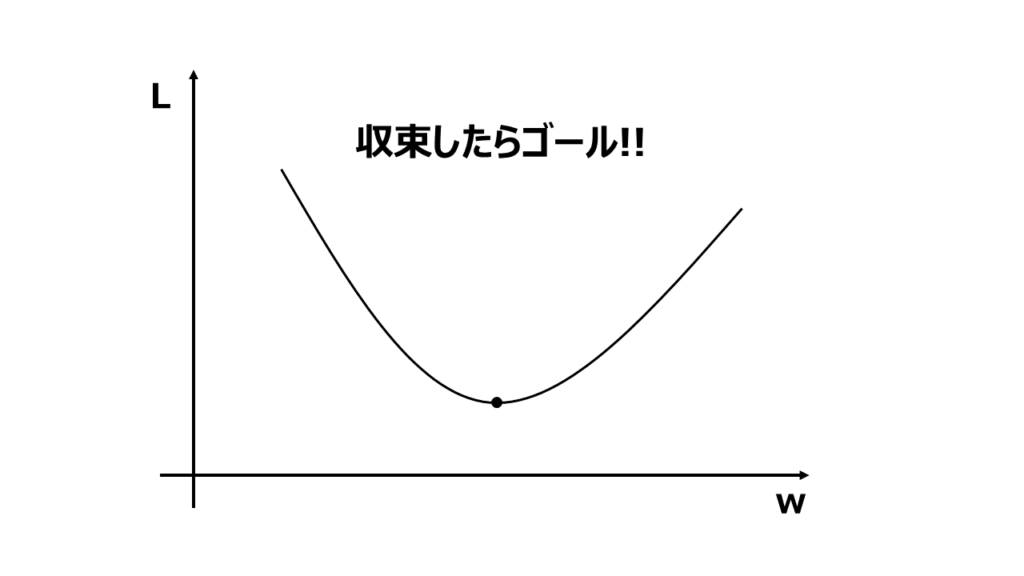
収束が達成されたら、最適化されたパラメータの値が得られます。これらの最適なパラメータは、モデルの学習や問題の最小化などの目的に応じて使用していきます。
勾配降下法の種類

勾配降下法にはいくつかの種類が存在します。以下に代表的な勾配降下法の方法の種類をいくつかご紹介します。
バッチ勾配降下法

一つ目はパッチ勾配降下法です。最急降下法の一つです。
バッチ勾配降下法は最も基本的な勾配降下法です。データセット全体を使用して損失関数の勾配を計算し、パラメータを更新します。
バッチ勾配降下法の特徴
バッチ勾配降下法は、データセット全体を使用するため、各パラメータの更新はデータセット全体の情報に基づいて行われます。
この方法は勾配の平均値を使用するため、各更新ステップでの方向がより確かであり、収束が安定します。
バッチ勾配降下法のメリット
バッチ勾配降下法のメリットは以下の通りです。
〇 バッチ勾配降下法は、収束が比較的早く、最適解に近づくことができます。
〇 データセット全体を使用するため、より正確なパラメータ更新が可能です。
〇 ミニバッチ勾配降下法と比較して、学習率のチューニングがより容易です。
バッチ勾配降下法のデメリット
続いてデメリットです。
× データセット全体を使用するため、メモリの要件が大きくなる場合があります。
× データセットが大規模な場合、計算時間が増える可能性があります。
× パラメータの更新ごとに計算が必要なため、高速化が困難な場合があります。
注意点
バッチ勾配降下法の注意点をまとめましょう。
・ バッチサイズを大きくすると、計算効率は向上しますが、収束が遅くなる可能性があります。
・ バッチサイズを小さくすると、計算効率は低下しますが、より急速な収束が期待できます。
バッチ勾配降下法は、小規模なデータセットやパラメータ更新の正確性が重要な場合に適しています。一方、大規模なデータセットや計算時間の制約がある場合には、次に紹介するミニバッチ勾配降下法や確率的勾配降下法などの手法が検討されます。
ミニバッチ勾配降下法

データセットを小さなバッチに分割して損失関数の勾配を計算し、パラメータを更新する手法です。
バッチ勾配降下法では全体を一括でやっていたのに対し、ミニバッチ勾配降下法では分割して行います。
ミニバッチ勾配降下法の特徴
ミニバッチ勾配降下法は、データセットをバッチに分割するため、各パラメータの更新は一部のデータに基づいて行われます。
ミニバッチのサイズは通常、数十から数百のデータポイントで構成されます。
ミニバッチ勾配降下法のメリット
ミニバッチ勾配降下法の利点です。
〇 ミニバッチ勾配降下法は、計算効率と収束のバランスを取ることができます。バッチサイズを適切に設定することで、高速な計算と効率的な収束が可能です。
〇 データセット全体を使用するバッチ勾配降下法よりもメモリ使用量が少なくなります。
〇 ミニバッチごとに勾配を計算するため、計算処理の並列化が容易です。
ミニバッチ勾配降下法のデメリット
デメリットも紹介しましょう。
× バッチサイズの選択が重要であり、小さすぎるとパラメータ更新の方向性が不安定になり、大きすぎると計算効率が低下する可能性があります。
× バッチサイズが小さい場合、ノイズの影響を受けやすくなり、局所解に陥りやすくなる可能性があります。
注意点
ミニバッチ勾配降下法の注意点をまとめましょう。
・バッチサイズの選択はトレードオフの問題であり、データセットの性質や問題の性質に応じて最適なバッチサイズを選ぶ必要があります。
・バッチサイズが小さい場合は、学習率の調整や学習スケジュールの設定が重要です。
ミニバッチ勾配降下法は、データセットが大規模であり、計算時間やメモリ使用量の制約がある場合に特に有用です。
確率的勾配降下法

確率的勾配降下法(Stochastic Gradient Descent, SGD)は、データセット全体ではなく、サンプルごとに勾配を計算してモデルパラメータを更新する手法です。
確率的勾配降下法の特徴
確率的勾配降下法は、データセット全体ではなく、サンプルごとの勾配を使用するため、計算効率が高いので計算コストが低くなります。特に大規模なデータセットにおいて有効です。
さらに、更新が頻繁に行われ、サンプルごとにパラメータが更新されるため、モデルが素早く収束することができます。
確率的勾配降下法のメリット
確率的勾配降下法のメリットのまとめです。
〇 データセット全体を使用せずに学習ができるため、メモリの制約がある場合でも扱うことができ大規模なデータセットに適用可能です。
〇 データがリアルタイムに到着する場合や、逐次的な学習を行う場合に有効でオンライン学習に適しています。
確率的勾配降下法のデメリット
デメリットのまとめです。
× 勾配の推定値にノイズが含まれるため、収束が不安定になることがあります。学習率の調整や学習のスケジューリングが重要です。
× 学習率やモーメンタムなどのハイパーパラメータの設定が重要であり、最適な値を見つけるための調整が必要です。
注意点
SGDではランダムにサンプルを選択するため、データの偏りがある場合には注意が必要です。偏りのあるデータによる学習のバイアスが生じる可能性があります。データの均衡性やバッチの作成方法に注意を払う必要があります。
その他の方法

これまで紹介した方法以外にもいくつかの種類があるので簡単に紹介したいと思います。
モーメンタム法
モーメンタム法は、勾配降下法に慣性項を追加することで、収束速度を向上させます。慣性項とは、前回の更新量を加算する項です。これにより、モーメンタム法は、勾配の方向に進むだけでなく、前回の更新量の方向にも進むようになります。これにより、収束速度が向上します。
AdaGrad
AdaGradは、勾配の変化量が大きくなるほど、パラメータの更新量を小さくします。これにより、勾配の変化量が大きいパラメータに過剰に学習しないようにします。
AdaGradは、深層学習において広く使用されている勾配降下法です。深層学習は、多くのパラメータを持つため、ほかの勾配降下法では収束速度が遅くなることがあります。AdaGradは、深層学習において、収束速度を向上させ、精度を向上させることができます。
RMSProp
RMSPropはAdaGradの収束に時間がかかるといった欠点を克服するために考案された方法です。
RMSPropは、勾配の二乗和を考慮してパラメータを更新します。これにより、RMSPropは、AdaGradに比べて、収束速度を向上させ、収束にかかる時間を短縮することができます。
Adam
Adamは、AdaGradとRMSPropの長所を組み合わせた勾配降下法の一種です。AdaGradは、勾配の方向に進むだけでなく、勾配の変化量を考慮してパラメータを更新する手法で、RMSPropは、勾配の方向に進むだけでなく、勾配の二乗和を考慮してパラメータを更新する手法です。Adamは、AdaGradとRMSPropの長所を組み合わせることで、収束速度と精度を向上させます。




コメント